inferential theory of learning
(Michalski, Sklar, Bloedorn, Kaufman, Wojtusiak)
This project aims at the development of the Inferential Theory of Learning (ITL) that views learning as a goal-oriented process of improving the learner’s knowledge by exploring the learner’s experience. The theory aims at understanding the competence aspects of learning processes, in contrast to the Computational Learning Theory that concerns their computational complexity. ITL addresses such questions as what types of inference and knowledge transformations underlie learning processes and strategies; what types of knowledge the learner is able to learn from a given input and from a given prior knowledge; what logical relationships exist among the learned knowledge, possible inputs and prior knowledge, etc.
The theory analyzes learning processes in terms of high level inference patterns called knowledge transmutations. Among basic transmutations are generalization, abstraction, similization, generation, insertion and replication. The central aspect of any transmutation is the type of underlying inference. If results of inference are found useful, then they are memorized. Thus, we have an “equation”:
Learning = Inferencing + Memorizing
Since learning processes may involve any possible type of inference, the ITL postulates that a complete learning theory has to encompass a theory of inference. To this end, we have attempted to identify and classify all major types of inference.
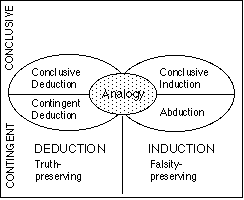
A Classification of Major Types of Inference
The figure above illustrates the proposed classification. The first criterion divides inferences into deductive and inductive. To explain them in a general way, consider the fundamental equation for inference: P ∪ BK |= C, where P stands for premise, BK for reasoner’s background knowledge, |= for entailment, and C for consequent. Deductive inference is deriving C, given P and BK, and is truth-preserving. Inductive inference is hypothesizing P, given C and BK, and is falsity-preserving.
The second classification divides inferences into conclusive (strong) and contingent (weak). Conclusive inferences involve domain-independent inference rules, while contingent inferences involve domain- dependent rules. Contingent deduction produces likely consequences of given causes, and contingent induction produces likely causes of given consequences. Analogy can be characterized as induction and deduction combined, and therefore occupies the central area in the diagram. Using this approach, we have clarified several basic knowledge transmutations, such as inductive and deductive generalization, inductive and deductive specialization, and abstraction and concretion. Generalization and specialization transmutations change the reference set of a description, and abstraction and concretion change its level-of-detail.
Selected References
Wojtusiak, J., Warden, T. and Herzog, O., “Machine Learning in Agent-based Stochastic Simulation: Inferential Theory and Evaluation in Transportation Logistics,” Computers & Mathematics with Applications, 64, 12, 3658-3665, 2012.
Michalski, R.S., “Inferential Theory of Learning: Developing Foundations for Multistrategy Learning,” in Machine Learning: A Multistrategy Approach, Volume IV, Morgan Kaufmann Publishers, 1994.
Michalski, R.S., “Inferential Theory of Learning as a Conceptual Basis for Multistrategy Learning,” Machine Learning, Special Issue on Multistrategy Learning, Vol. 11, pp. 111-151, 1993.
Michalski, R.S., LEARNING = INFERENCING + MEMORIZING: Basic Concepts of Inferential Theory of Learning and Their Use for Classifying Learning Processes, in Cognitive Models of Learning, Chipman, S. and Meyrowitz, A. (Eds.), 1992.
For more references, see publications section.
